代码随想录和牛客刷题

解题代码：

$$(n-p o s) * t_{c} \leq M$$

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

int main()
{
    int n, Q, tc;
    ios::sync_with_stdio(false);
    cin >> n >> Q >> tc;
    vector<ll> t(n + 1);
    for(int i = 1; i <= n; i ++)
        cin >> t[i];
    sort(t.begin(), t.end());
    for(int i = 1; i <= n; i ++)
        t[i] += t[i - 1];
    while(Q --)
    {
        ll M;
        cin >> M;
      //（n - pos）* tc <= M
        ll c = min((ll)n, M / tc);//防止越界
        ll ans = t[n - c] + tc;
        cout << ans << '\n';
    }
    return 0;
}

解题思路：

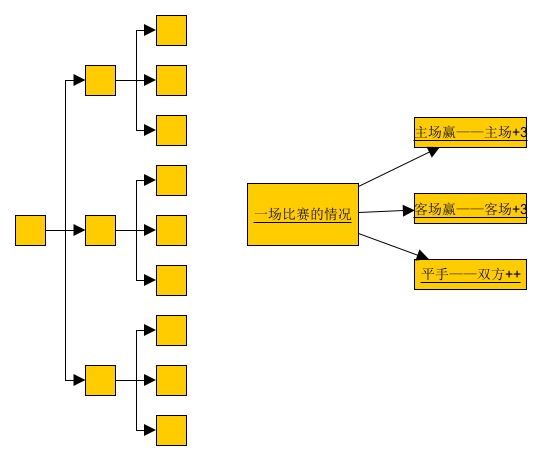
• 对于每一场情况都有3种情况出现，比如下面这种就是2场比赛就有9种情况出现。我们所要做的是，遍历这9种情况。事实上，可以先定义一个pw3[]数组，记录当打了m场时一共有多少种情况，然后依次遍历即可。在每次遍历的时候，设置一个maxn变量记录id最小的情况，最终遍历完后所得到的即为第一只鸡的最小的id情况。

相应的代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 15;
int pw3[N];
int a[N],u[N],v[N];

void solve(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>u[i]>>v[i];
    int maxn = n;  // 用来记录id最小的时候的取值
    for(int i=0;i<pw3[m];i++){
        
    }
}

void init(){
    pw3[0] = 1;
    for(int i=1;i<=N) pw3[i] = 3*pw3[i-1];
}

int main()
{
    int t;
    cin>>t;
    init();
    while(t--){
        solve();
    }
    return 0
}

难哭了QAQ~~

思路：

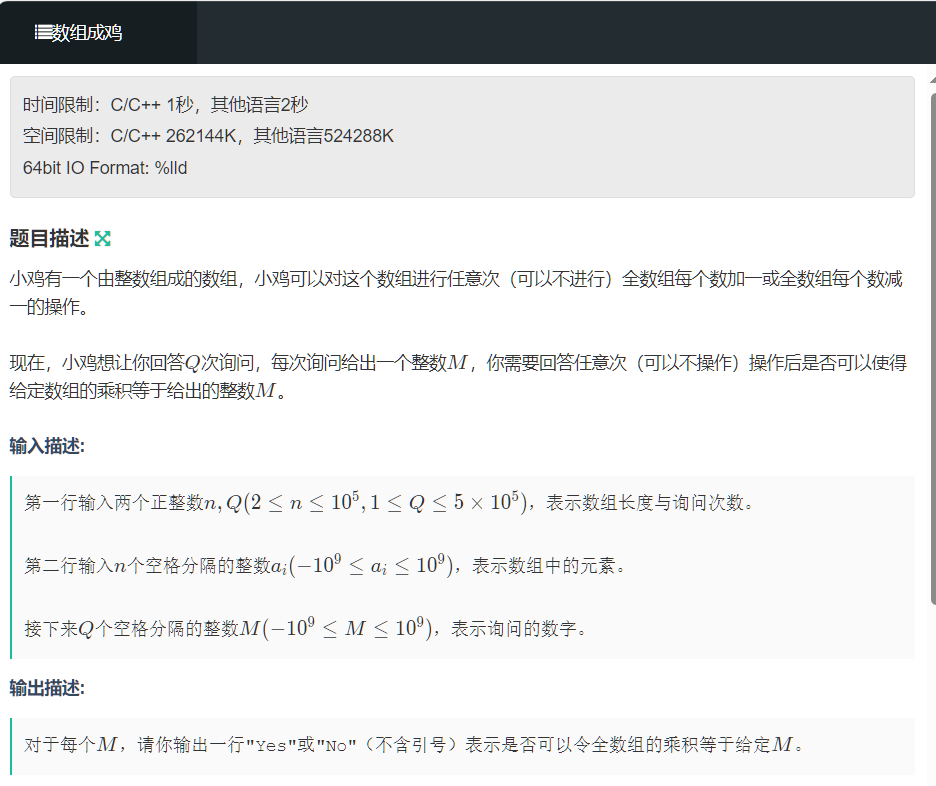
疯狂遍历所有的情况，然后把它存到set里面（这里就要考虑到如何将每一种情况i都遍历一遍了，好巧妙QAQ），然后对于每次询问，只要看它是否在set里面即可。遍历的方法：

• 减1的情况：每遍历一个数组元素a[i]，就整个数组元素都减去它，相当于每个数组元素都执行了a[i]次减减，然后在这基础上再继续减减，直到超出了所指定的范围-1e9，这是就把减减的所有情况都搞出来了，并存入到了set里面
• 加1的情况：每遍历一个数组元素a[i]，就整个数组元素都加上它，相当于每个数组元素都执行了a[i]次加加，然后在这基础上再继续加加，直到超出了所指定的范围1e9，这是就把加加的所有情况都搞出来了，并存入到了set里面

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
constexpr int Inf = 1e9,N = 2e5 +10;

ll a[N]; // 数据范围
int n;  // 实际用的数据空间
set<int>s;

bool check(ll x){
    ll res = 1;
    for(int i=1;i<=n;i++){
        res *= a[i]+x;
        if(llabs(res)>Inf) return false;
    }
    s.emplace(res); // 如果不会超出范围的话，就把它存入set中，其实这里不用set数据结构也是可以的，只不过是效率问题，用vector的find也可以
    return true;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int q,M;
    cin>>n>>q;
    ll l,r;
    for(int i=1;i<=n;i++) cin>>a[i];
    s.emplace(0);
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++){
        if(a[i] == a[i-1]) continue; // 就是因为当它相等的时候，先前的一个结果就已经搞定了，再来一个同样的数据的话其实是等效的
        for(l = -a[i]-1;check(l);l--);
        for(r = -a[i]+1;check(r);r++);
    }
    while(q--){
        cin>>M;
        cout<<(s.count(M)?"Yes\n":"No\n");  // 结果M是否存在set中，这个set就是把所有的结果都存了起来
    }

    return 0;
}

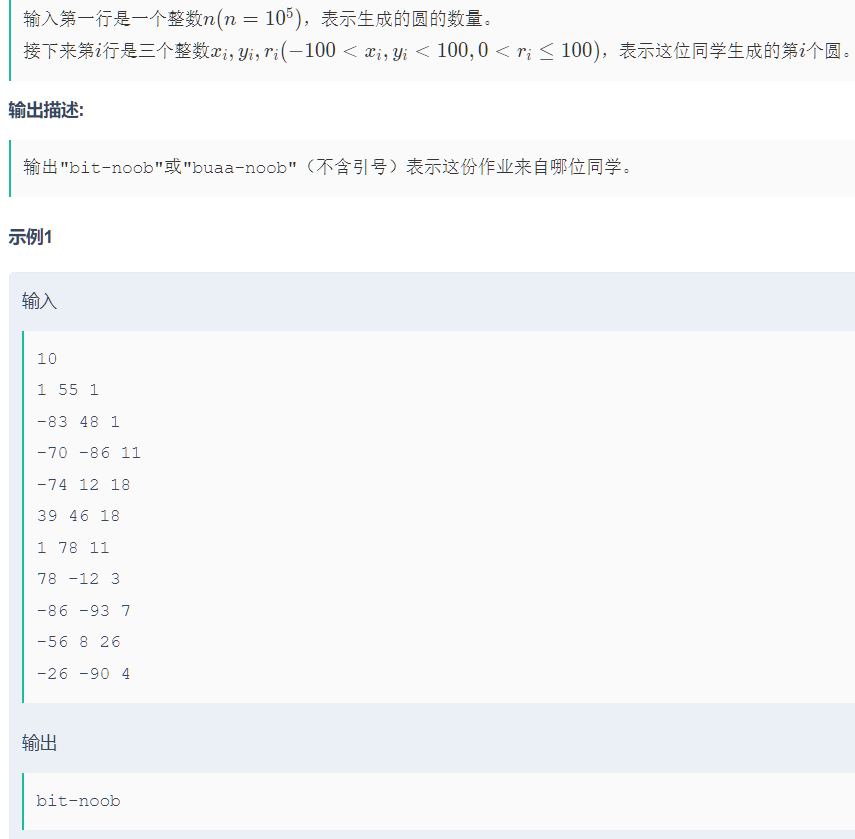
好家伙，玩起了概率题？

• 代码如下

  #include "bits/stdc++.h"
  
  using namespace std;
  using i64 = long long;
  
  int main() {
      ios::sync_with_stdio(false);
      cin.tie(nullptr);
      
      int n;
      cin >> n;
  
      int ans = 0;
      for (int i = 0; i < n; i++) {
          int x, y, r;
          cin >> x >> y >> r;
          if (x <= 9 && x >= -9 && y <= 9 && y >= -9) {
              ans++;
          }
      }
      
      if (ans <= n / 90) {
          cout << "bit-noob\n";
      } else {
          cout << "buaa-noob\n";
      }
  
      return 0;
  }

  好玩，简单题

  

解题思路：

这道题就是先理想状态下，每只猫的周围都是空的。然后就看是否存在两只猫挨在一起的情况，如果有的话就减一。这里判断两只猫是否挨在一起的方法是直接定一个走路方案数组，然后遍历其四周，看看其四周是否有猫。

代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[505][505];
int direct[4][2]{
    {-1,0},
    {0,-1},
    {1,0},
    {0,1}
};
int main()
{
    int n,m,k;
    cin>>n>>m>>k;
    int ans = 0;
    for(int i=1;i<=k;i++){
        int x,y;
        cin>>x>>y;
        a[x][y] = 1;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j] == 0) continue;
            for(int z=0;z<4;z++){
                ans+=a[i+direct[z][0]][j+direct[z][1]];
            }
        }
        
    }
    cout<<4*k-ans/2<<endl;
    return 0;
}

解题思路：

直接从右边看起，按照他说的那样，如果遇到不相同的，直接步数加加后，删去后面的宝石即可。然后最终会遇到剩下前面开头连续相同的几个宝石，这时候就只能够一个一个的宝石这样删除了。而且这个版本就两种宝石颜色而已。

代码如下

// 太聪明了！！！QAQ
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int a[N];
int main()
{
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
    
        for(int i=1;i<=n;i++) cin>>a[i];
        int ans = 0;
        int now = n;
        for(int i=n;i>=1;i--){
            if(a[i]!=a[now]){
                ans++;
                now = i-1;
            }
        }
        for(int i=1;i<=now;i++){
            // if(a[i]!=a[1]) break;
            ans++;
        }
        cout<<ans<<endl;
    }
    return 0;
}

困难版：

解题思路：

现在相当于宝石的颜色不再是2种了，而是有最多n种，然后先得到各种颜色的最后一次出现的下标，然后再得到这些下标中最小的那一个，作为一次删除的起点，然后后续思路都是一样的逻辑。

需要注意的是，考虑一下完成这一想法的数据结构，可以直接用vector来存数据。

代码如下：

// 太聪明了！！！QAQ
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10;
int a[N];
vector<int> pos[N];
int main()
{
    int t;
    cin>>t;
    while (t--)
    {
        int n;
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>a[i];
            pos[i].clear();
        }
        for(int i=1;i<=n;i++){
            pos[a[i]].push_back(i);
        }
        int mn = n;
        for(int i=1;i<=n;i++){
            if(pos[i].size()) mn = min(mn,pos[i].back());
        }
        int ans = 0;
        int now = mn;
        int pre = n;
        while(pre>=1){
            ans++;
            mn = now;
            for(int i=pre;i>=now;i--){
                pos[a[i]].pop_back();
                if(pos[a[i]].size()) mn = min(mn,pos[a[i]].back());
            }
            pre = now -1; // 逐步收缩,记住这里的顺序，先步数++，然后再进行收缩，这样就不存在步数缺了的情况了
            now = mn;  // 更新了现有颜色中各种颜色的最后下标的最小的那个下标
        }
        cout<<ans<<endl;
    }
    return 0;
}

347. 前K个高频元素

解题思路：通过创建map数据结构，方便统计每个数据出现的频率，然后利用最小堆将数据进行存储（之所以用最小堆是因为每当这个堆所存储的元素数量超过K个的时候，就可以把top给 删掉，最终就只会留下频率为前K个的元素），这道题的关键在于学会运用数据结构进行数据的处理。

需要额外注意的一点是：重载运算符必须要求存在类对象，不能直接传入两个类指针参数比较。可以通过重写operator函数，然后将其封装在新建的一个类内，然后再在priority_queue中将所创建的类作为其第三个参数传进去即可。

相应的代码如下：

class Solution
{
public:
    class myCompare
    {
    public:
        bool operator()(const pair<int, int> &lhs, const pair<int, int> &rhs)
        {
            return lhs.second > rhs.second;
        }
    };

public:
    vector<int> topKFrequent(vector<int> &nums, int k)
    {
        unordered_map<int, int> map;
        for (int i = 0; i < nums.size(); i++)
        {
            map[nums[i]]++;
        }

        // 此时需要创建一棵最小堆出来才可以
        priority_queue<pair<int, int>, vector<pair<int, int>>, myCompare> q;
        for (unordered_map<int, int>::iterator it = map.begin(); it != map.end(); it++)
        {
            q.push(*it);
            if (q.size() > k)
            {
                q.pop();
            }
        }

        vector<int> result(k);
        for (int i = k - 1; i >= 0; i--)
        {
            result[i] = q.top().first;
            q.pop();
        }

        return result;
    }
};