图灵兼职遇到的有趣题目

图灵班

在从小到大的排序数组中，

lower_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于或等于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

控制格式化输出

时刻要记住，控制输出的位数的代码如下：

cout<<setiosflags(ios::fixed)<<setprecision(3)<<distance;

vector查找元素

#include <iostream>  
#include <vector>  
#include <algorithm>  // for std::find  
  
int main() {  
    std::vector<int> numbers = {1, 2, 3, 4, 5};  
    int target = 3;  
    auto it = std::find(numbers.begin(), numbers.end(), target);  
  
    if (it != numbers.end()) {  
        std::cout << "Found " << target << " at index " << it - numbers.begin() << std::endl;  
    } else {  
        std::cout << target << " not found" << std::endl;  
    }  
    return 0;  
}

使用哈希表的时机

​ 当我们需要查询一个元素是否出现过，或者一个元素是否在集合里的时候，就要第一时间想到哈希法。

辗转相除法

#include<bits/stdc++.h>
using namespace std;
int digui(int a,int b){
	if(b==0) return a;
	else return digui(b,a%b);  // 这样的话，传进去的a%b一定是比b小的
}

int main(){
	int a,b;
	cin>>a>>b;
	cout<<digui(a,b)<<endl;
	return 0;
}

递归值得学习的题目

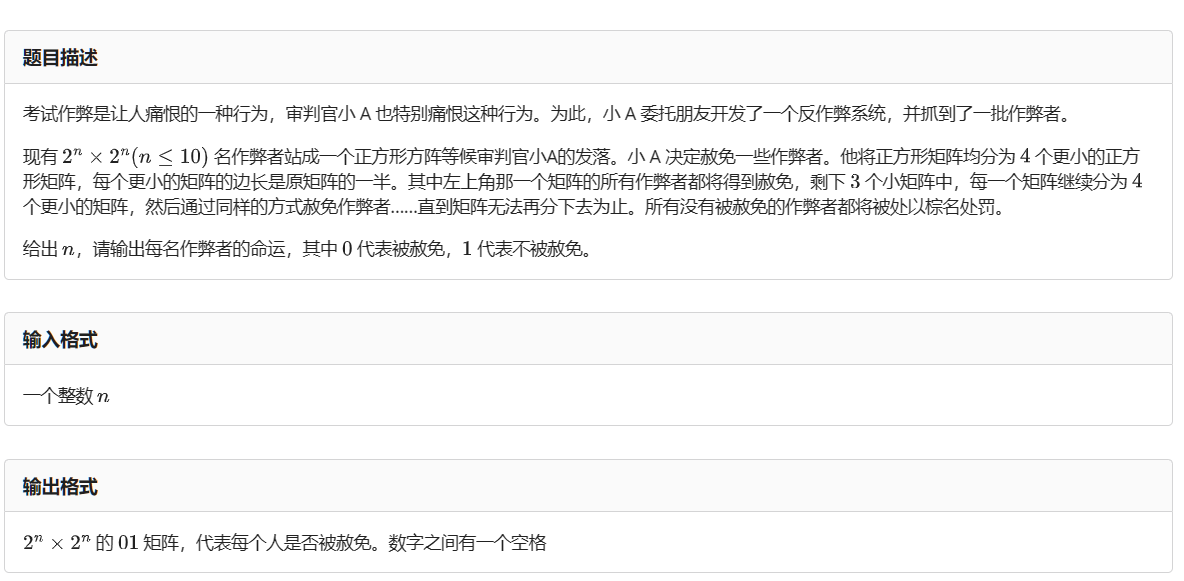
代码如下：

// 显然，容易思考整个数组的情形，但是需要意识到，就算每次你递归的时候用的是整个数组的传递，归根到底还是对所传入的数组中的元素的索引的逻辑
#include<bits/stdc++.h>
using namespace std;
int a[1025][1025];

void digui(int x,int y,int n){
	if(n==1){
		a[x][y] = 1;
		return;
	}
	else{
		digui(x,y+n/2,n/2);
		digui(x+n/2,y,n/2);
		digui(x+n/2,y+n/2,n/2);
	}
}
int main(){
	int n;
	cin>>n;
	n = (1<<n);
	digui(0,0,n);	
	for(int i=0;i<n;i++){
		for(int j=0;j<n;j++){
			cout<<a[i][j]<<' ';
		}
		cout<<endl;
	}
	return 0;
}

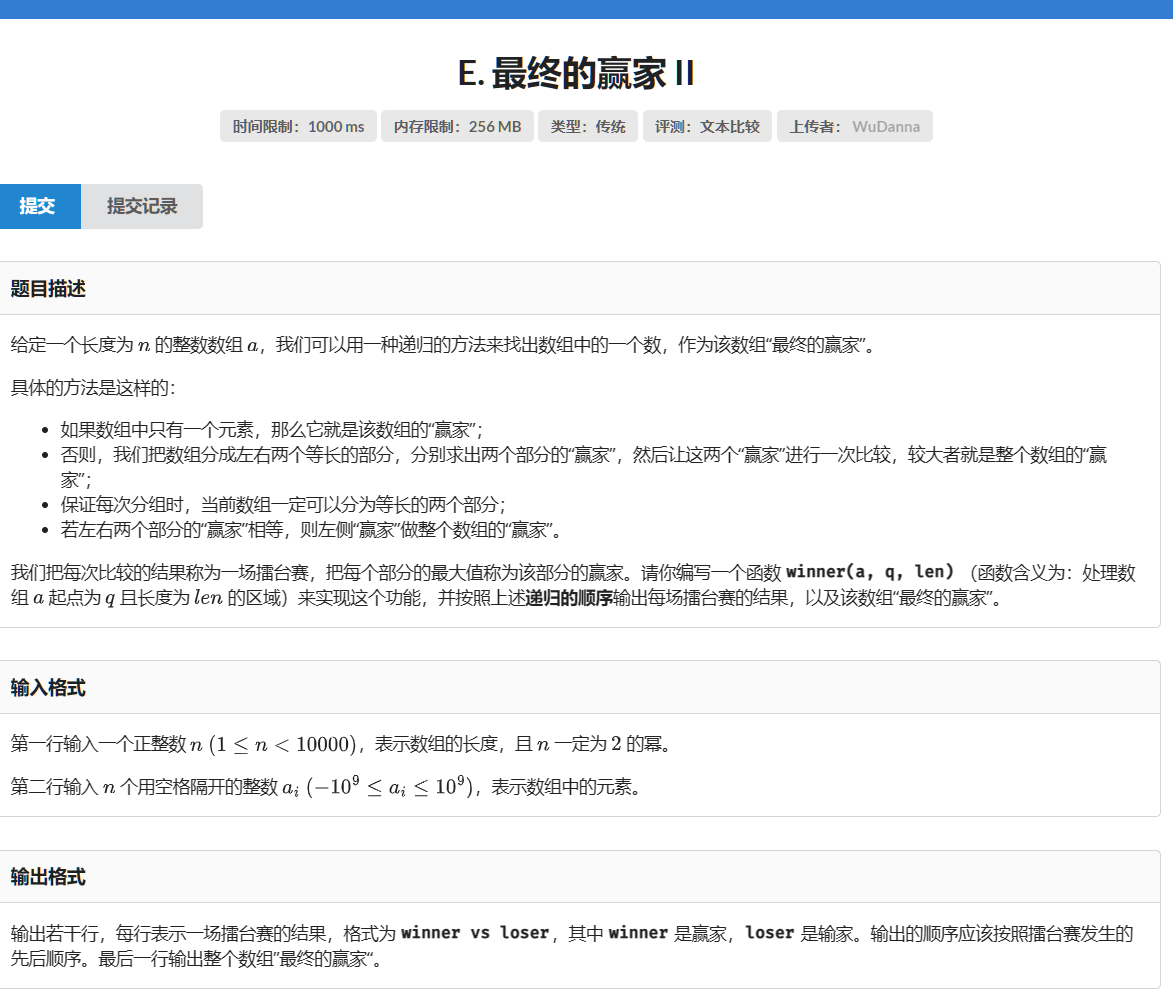
代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[10005];

int digui(int *a,int begin,int end){
	if(begin == end) return a[begin];
	else{
		int half_len = end/2+end%2;
		int left = digui(a,begin,(begin+end)/2);  // 其实就是不断地收缩区域，从而得到左边和右边的想要得到的值
		int right = digui(a,(begin+end)/2+1,end);
		if(left>=right){
			cout<<left<<" vs "<<right<<endl;
			return left;
		}
		else{
			cout<<right<<" vs "<<left<<endl;
			return right;
		}
	}
}

int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	cout<<digui(a,1,n)<<endl;
	return 0;
}